
平方四辺形の面積 小5の問題です 斜線部の面積を求めます 答えは14 小学校 教えて Goo
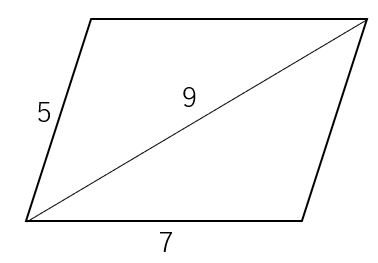
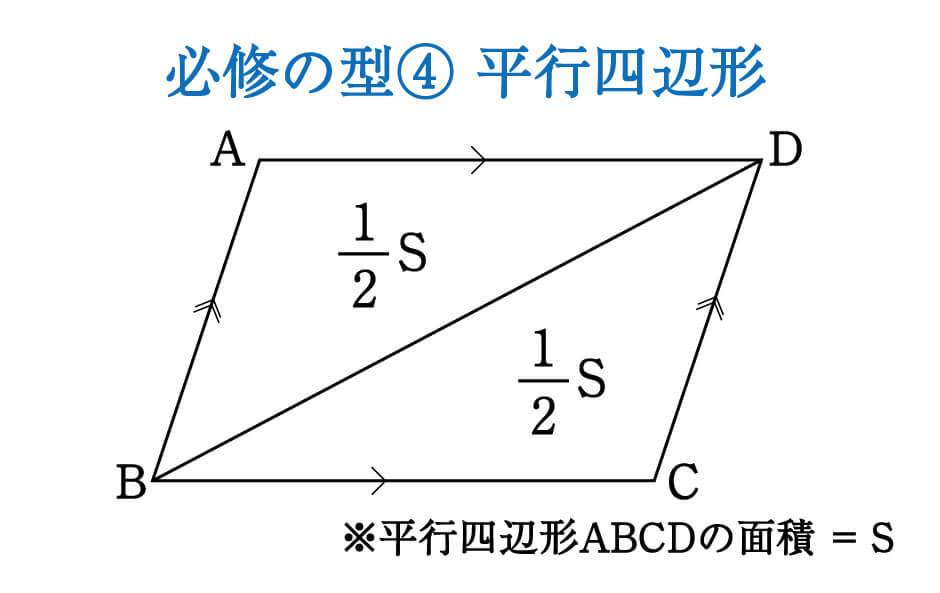
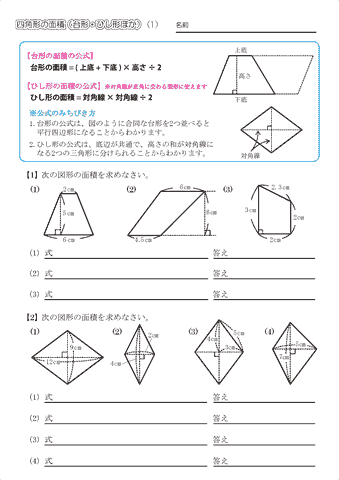
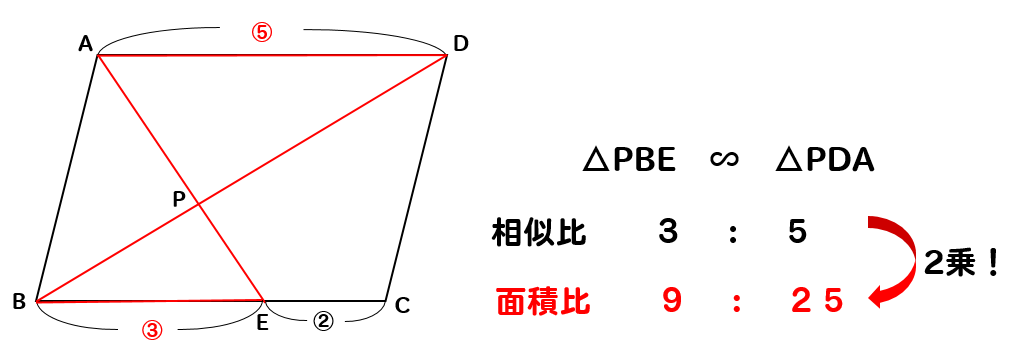
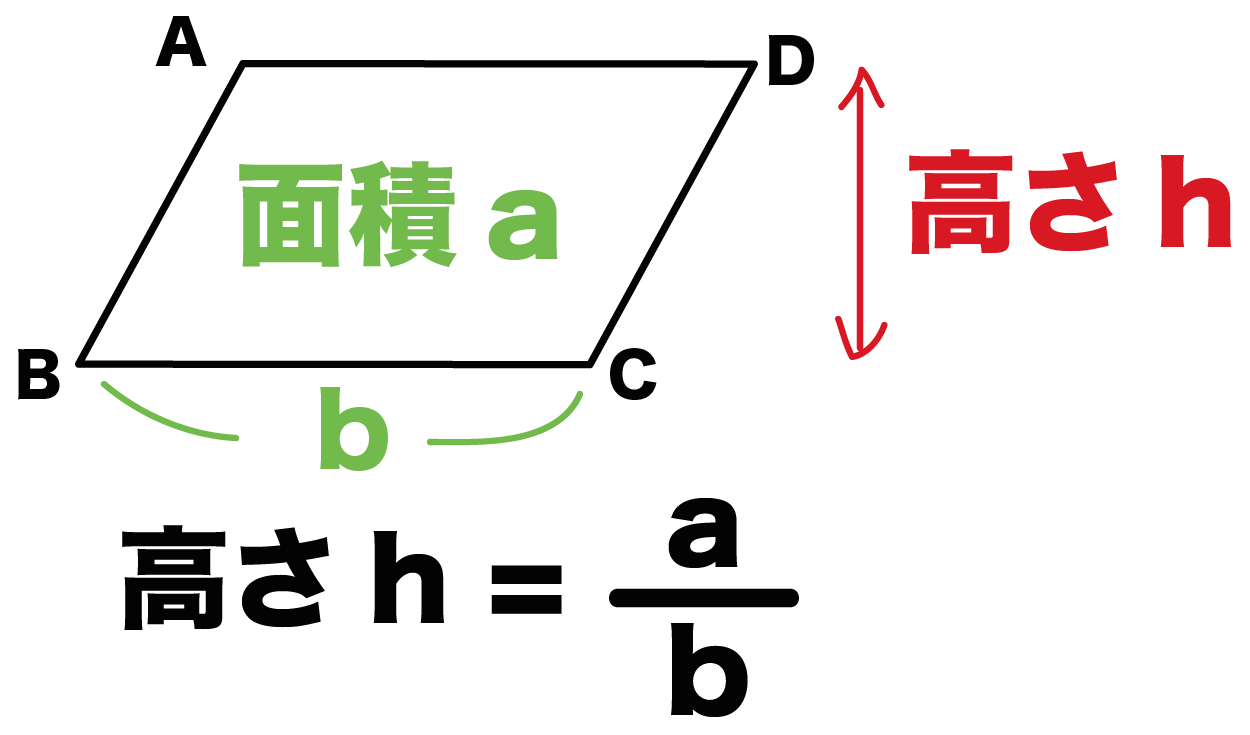
ひし形の面積は 2 2 つの対角線の長さをかけて2で割ったもの、つまり 『対角線×対角線÷2 ÷ 2 』 で求めることができます。 平行四辺形の一種でもあるので、底辺と高さが分かっていれば『底辺×高さ』でも求められます。 たとえば以下のような問題の場合 こんにちは。平行四辺形と面積②です。それではどうぞ。 面積比の問題で, 1つの攻略方法として, 相似比の2乗から攻める方法を紹介しておりますが, 相似な関係がない場合は, 役に立ちません。そこで, 相似な関係がなくてもで
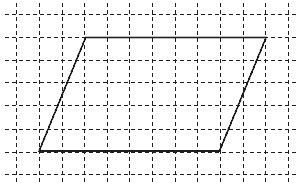
平行四辺形 面積 問題
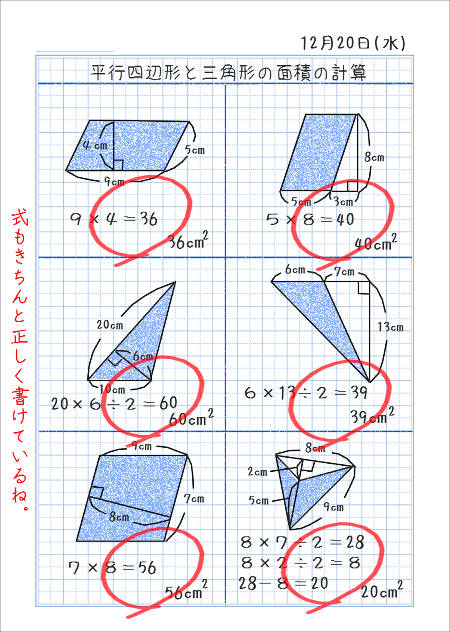
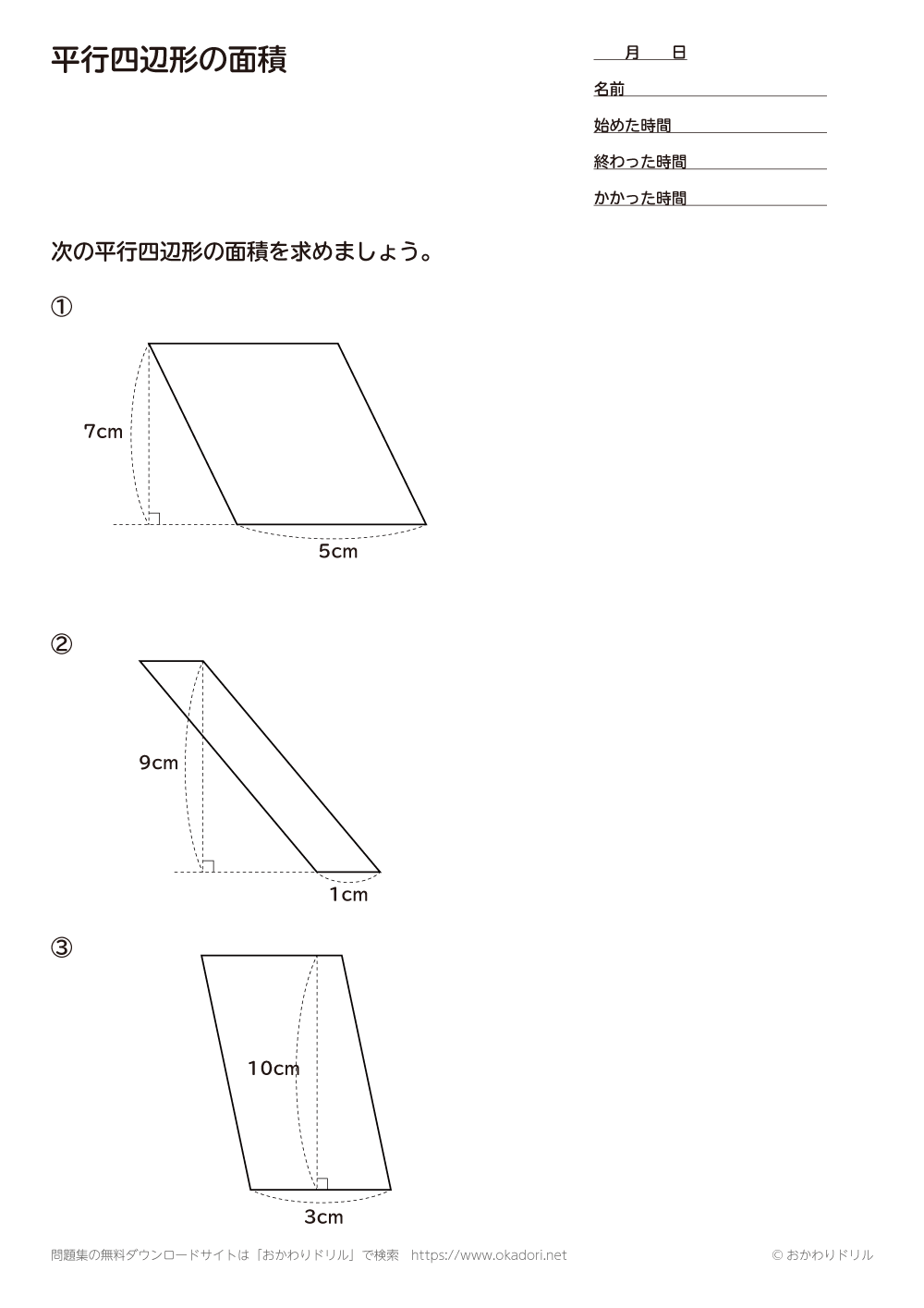
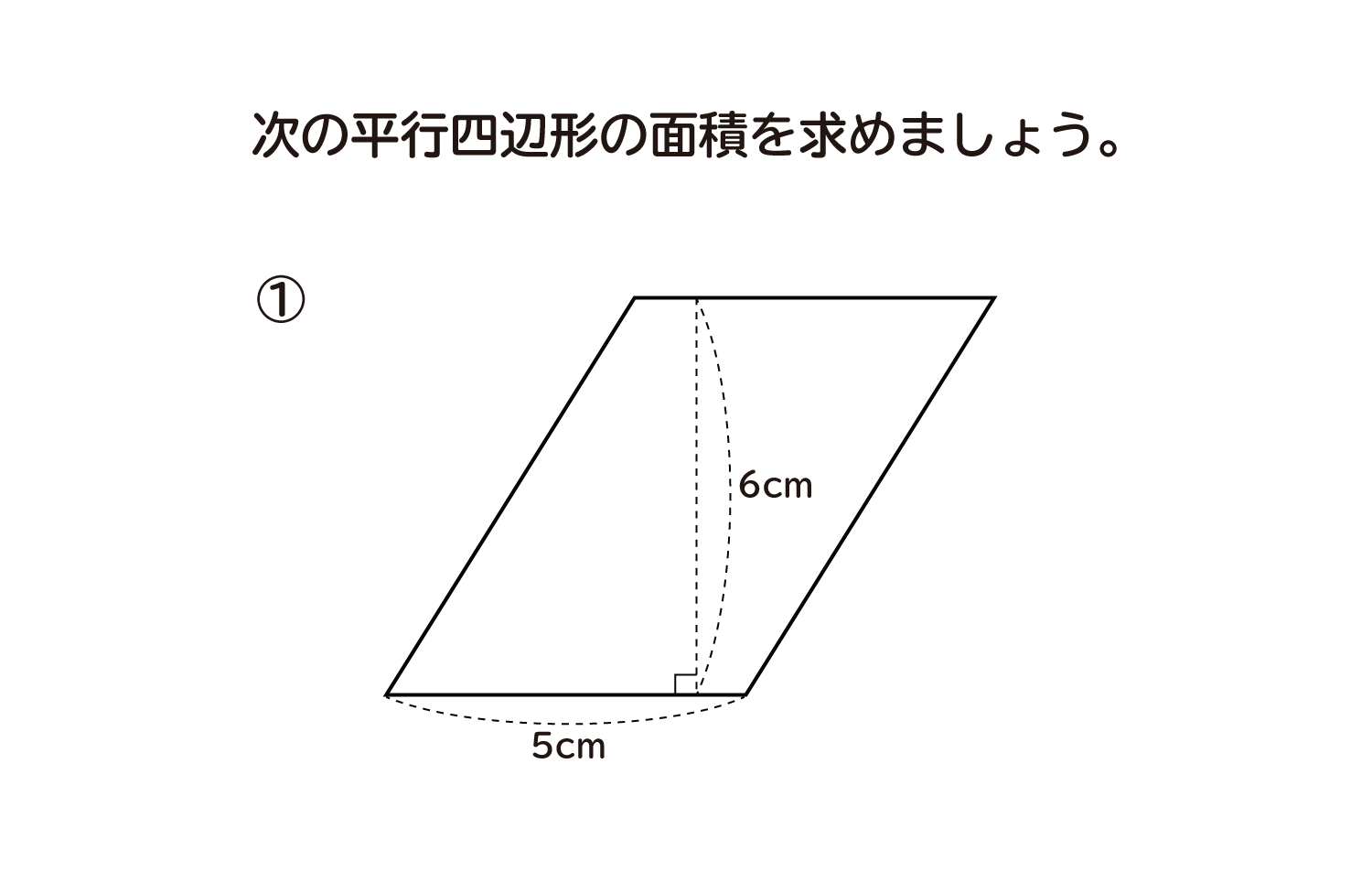
平行四辺形 面積 問題-第292問 平行四辺形の面積 図形ドリル 5年生 6年生 平行四辺形 相似 相似比 面積比 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。三角形 面積問題 平行四辺形 面積 図形問題 小学5年生 平行四辺形の面積もんだいは、底辺と高さを求めそれぞれを掛けるだけです すなわち 公式 底辺×高さ です 考え方は、面積のプリント①で説明してい
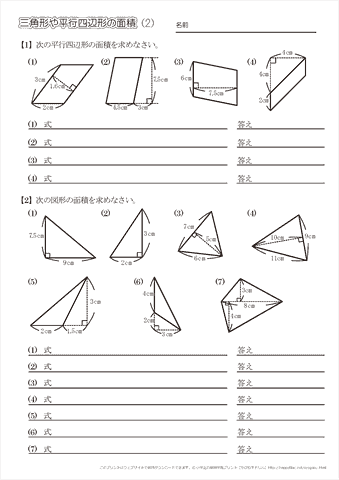
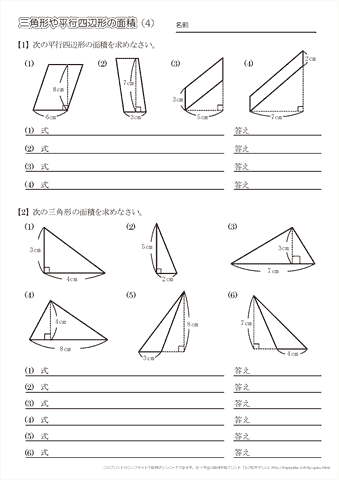
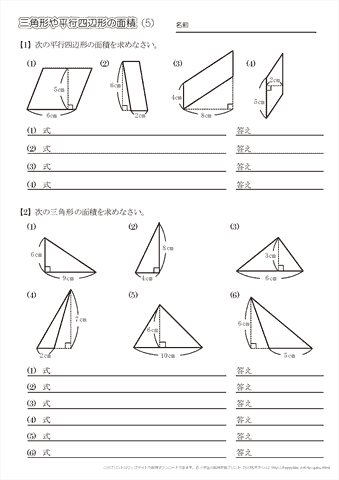
小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生
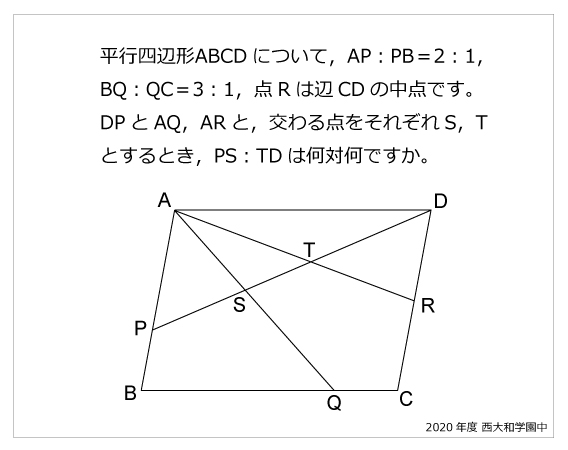
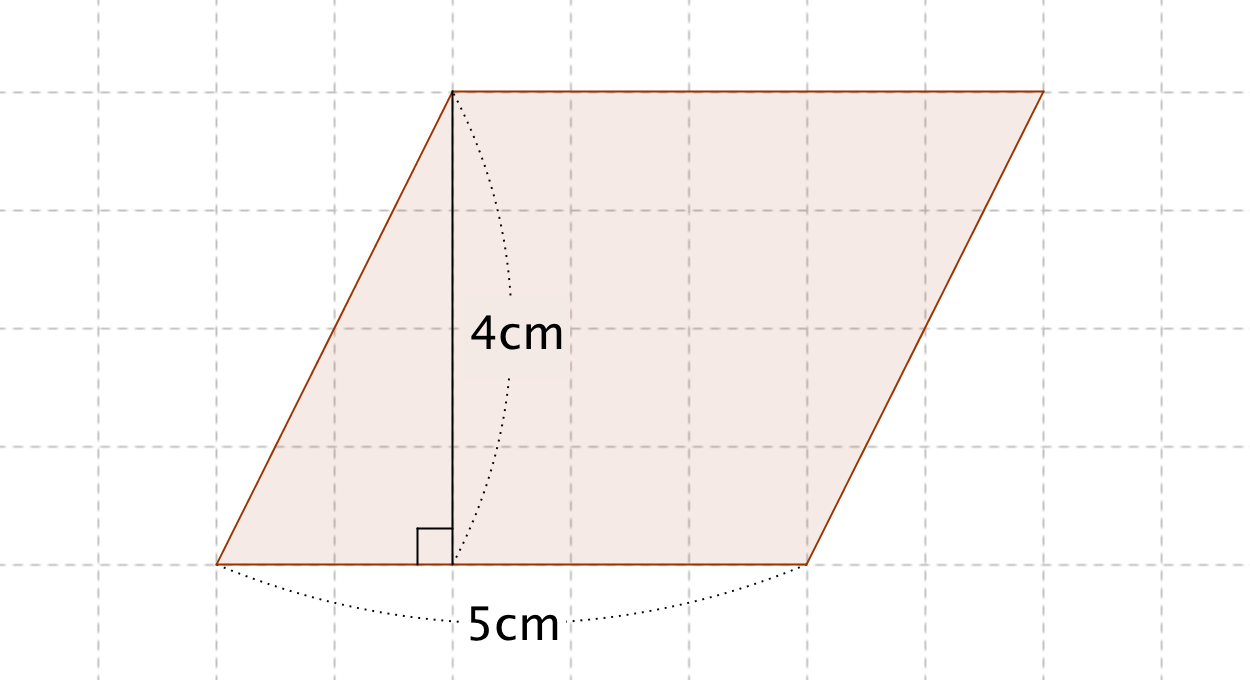
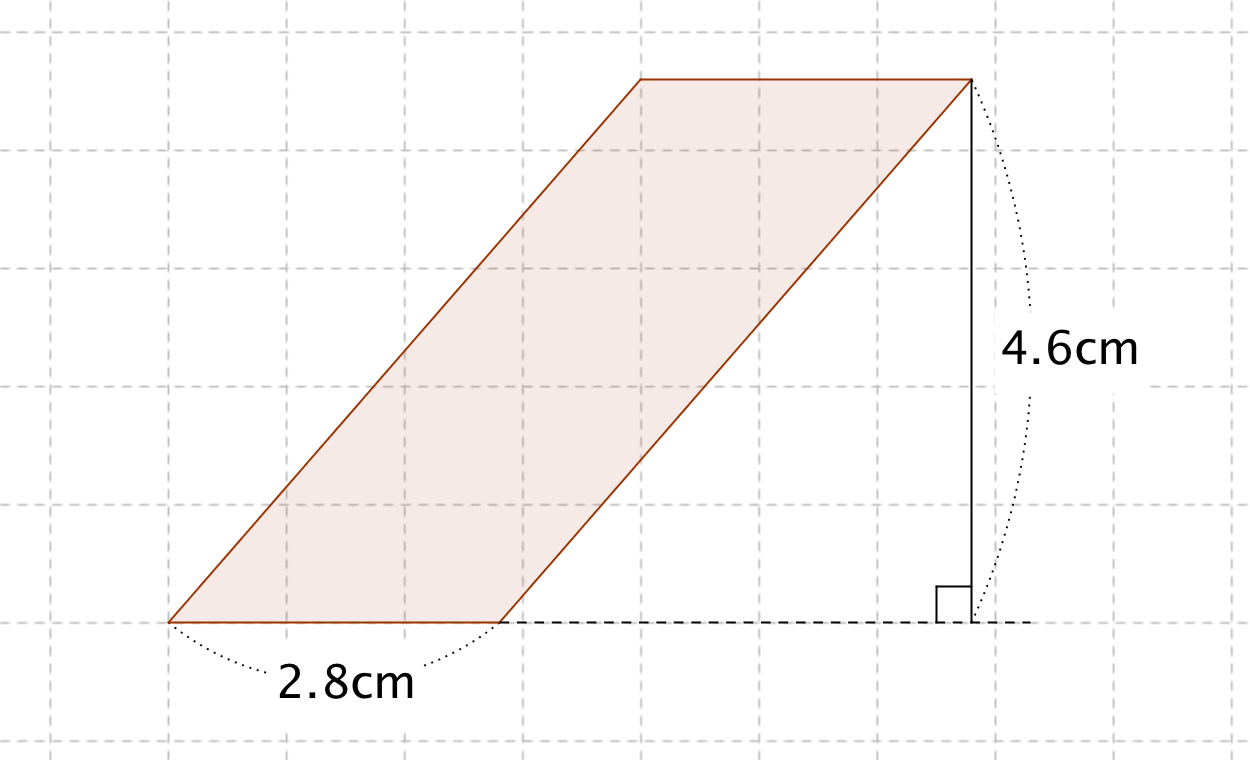
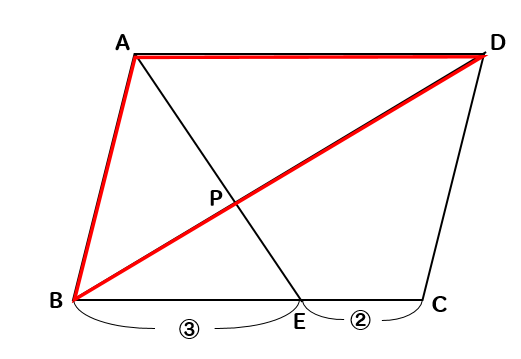
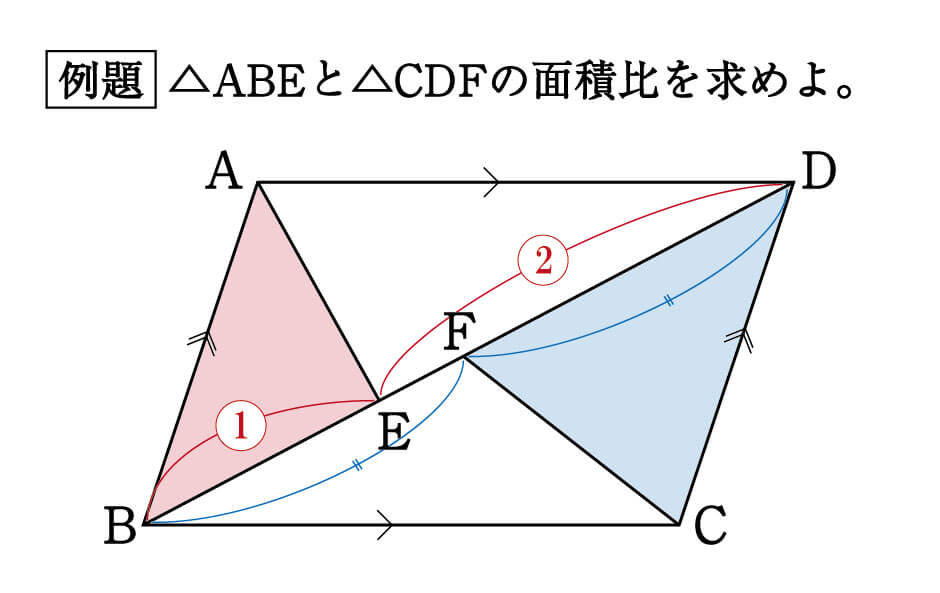
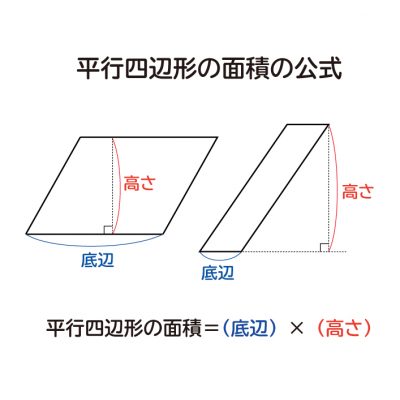
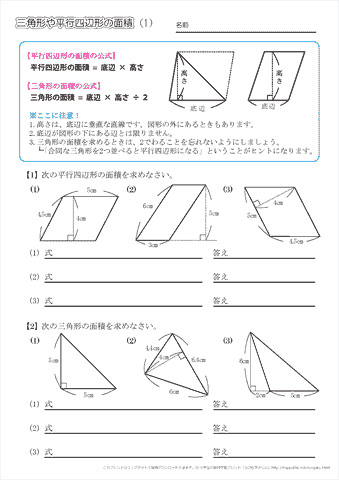
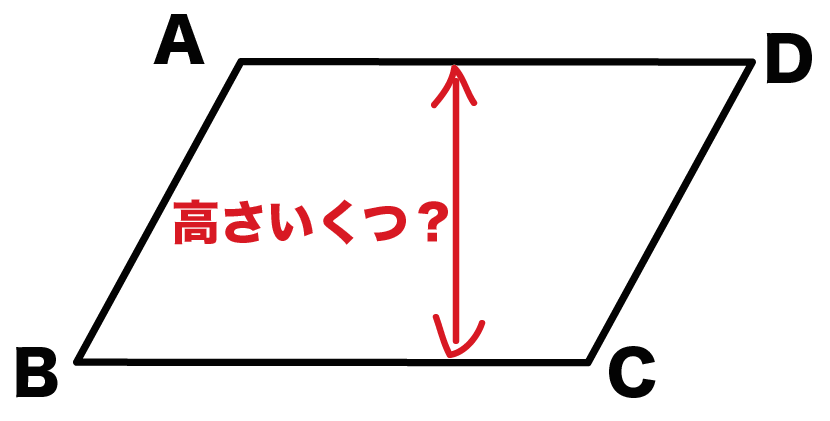
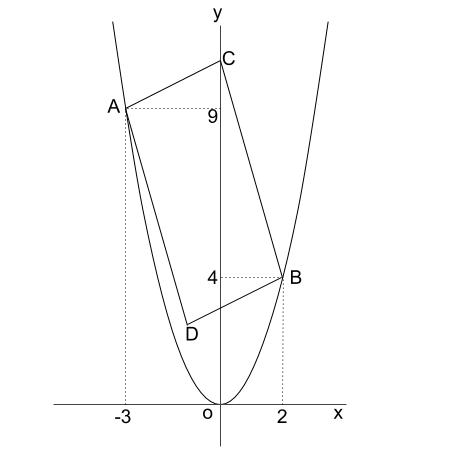
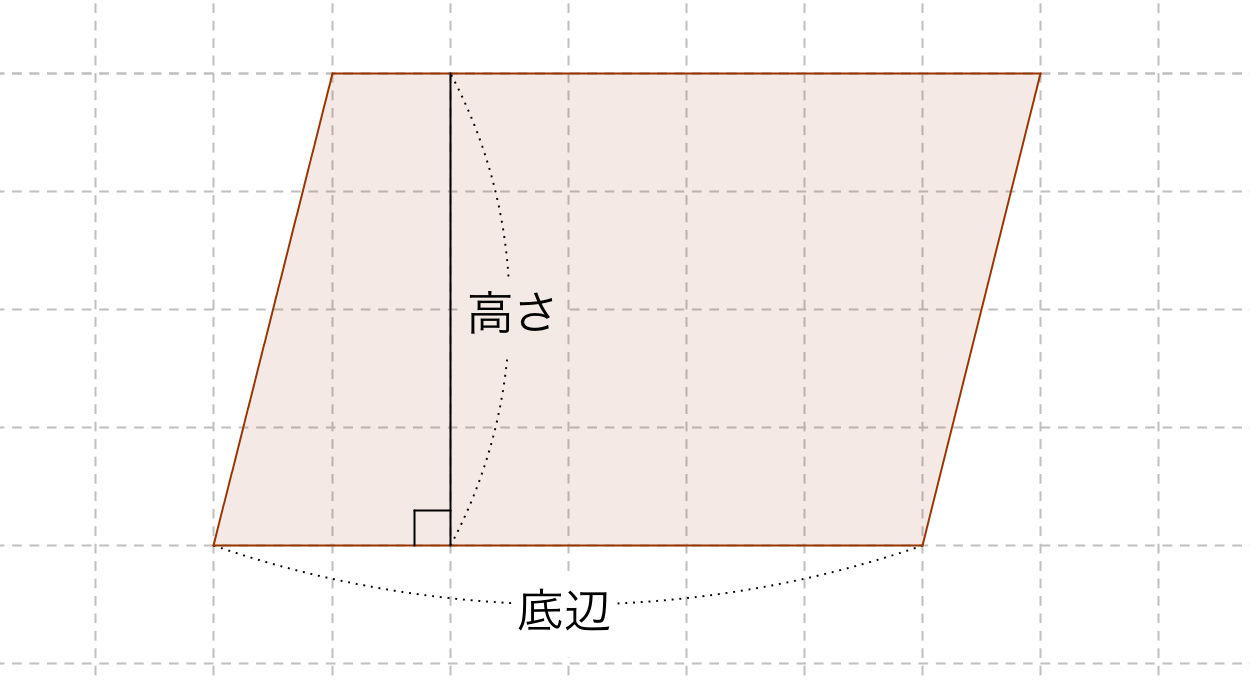
平行四辺形の面積の問題です。 公式は難しいものではありませんが、底辺と高さをしっかり理解するようにしてください。 ポイント 平行四辺形の1つの辺を底辺とするとき、底辺に向かい合う辺まで垂直にひいた直線の長さを高さといいま相似比の練習問題(平行四辺形1) 問1.次の各問いに答えなさい。 (ア) abcd においてae:ed =2:1 で efd の面積が2 cm 2のとき (1) cfd の面積 (2) bcf の面積 (3) abcd の面積 (イ)右の平行四辺形abcd で、辺ab の中点をe、対角線bd とce の交点をf とするとき 目次 平行線と三角形の面積 等積変形の作図 ①四角形から三角形を作る ②折れ線を直線にする ③五角形から三角形を作る 等積変形の利用① (平行四辺形の中の三角形) 等積変形の利用② (面積を求める) 平行線と面積 (等積変形)のまとめ
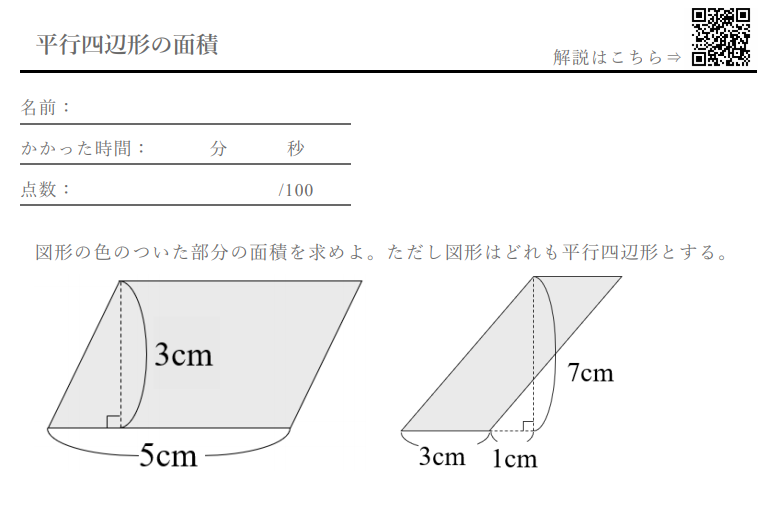
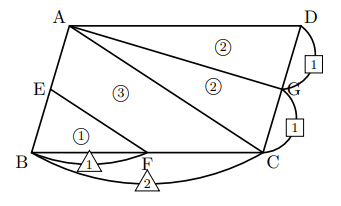
平行線と面積に関する問題です。ポイント平行線と面積に関する問題は以下のことをしっかり確認しておきましょう。平行線にはさまれた三角形の面積は等しい面積が等しい三角形の頂点を通る直線は平行例)下の図で abcと dbc面積が等しい → abc= dbc とかく。平行四辺形 面積 図形問題 小学5年生平行四辺形の面積もんだいは、底辺と高さを求めそれぞれを掛けるだけですすなわち 公式 底辺×高さ です考え方は、面積のプリント①で説明しています平行四辺形 面積問題①平行四辺形 面積問題②平行四辺形面積の平行四辺形の性質 パワーポイント教材(348k) ワークシートパック 平行四辺形になる条件 パワーポイント教材(163k) ワークシートパック 平行線と面積 パワーポイント教材(292k) ワークシートパック 5章 章末問題 パワーポイント教材(k)
平行四辺形 面積 問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「平行四辺形 面積 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「平行四辺形 面積 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「平行四辺形 面積 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | 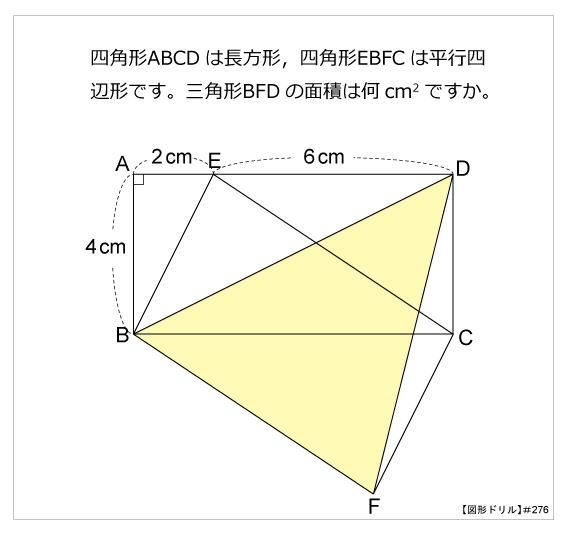 |
「平行四辺形 面積 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | 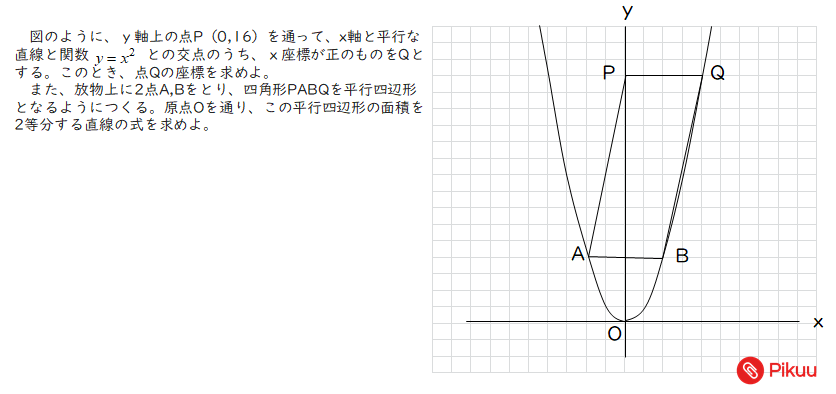 |
 |  | |
「平行四辺形 面積 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 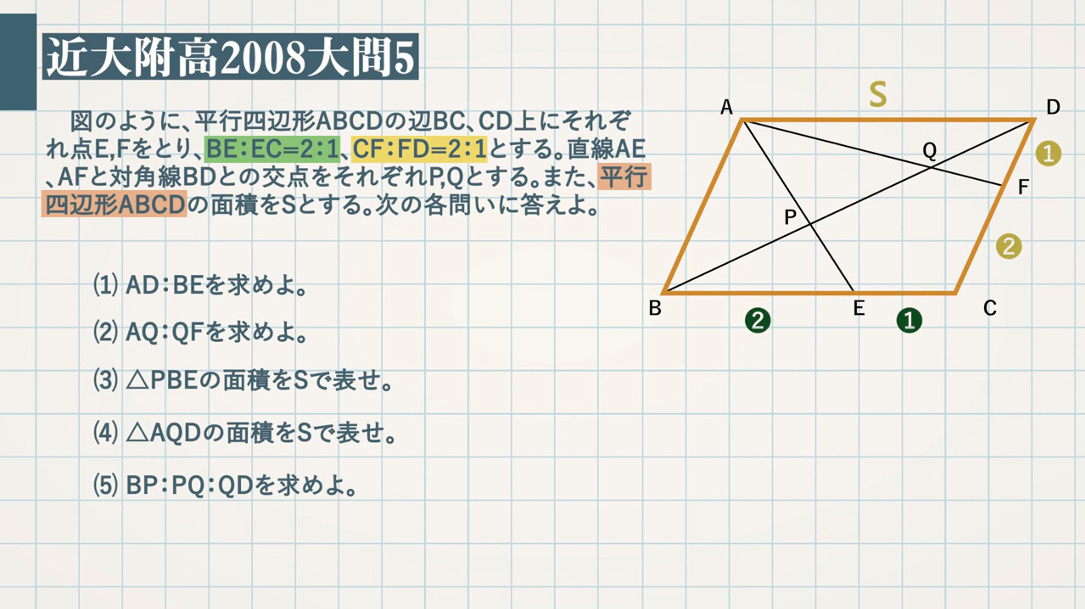 |  |
 | 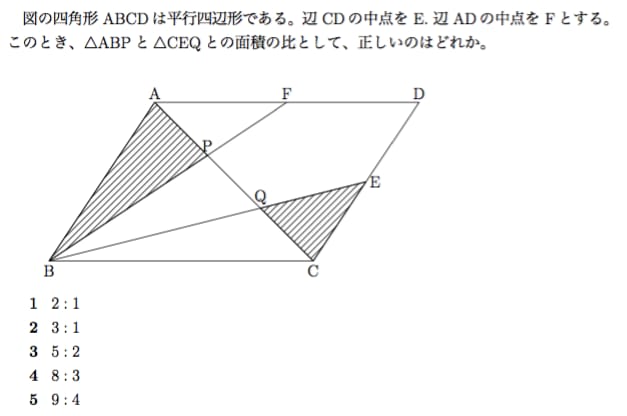 | |
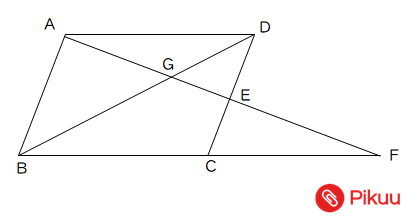 |  |  |
「平行四辺形 面積 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
「平行四辺形 面積 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「平行四辺形 面積 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | 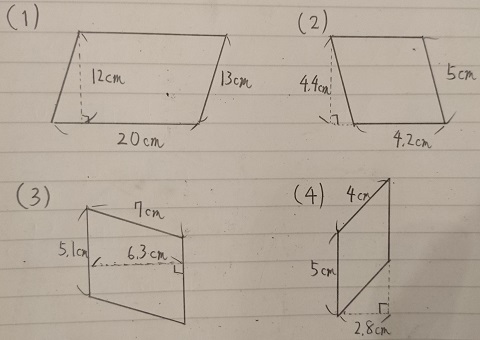 |
 |  | 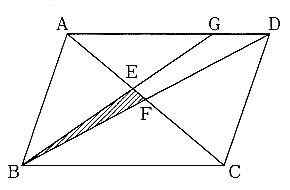 |
「平行四辺形 面積 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 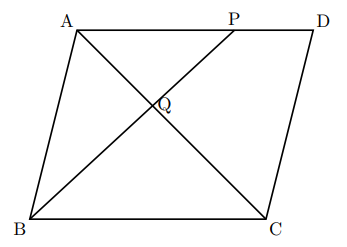 | |
 | 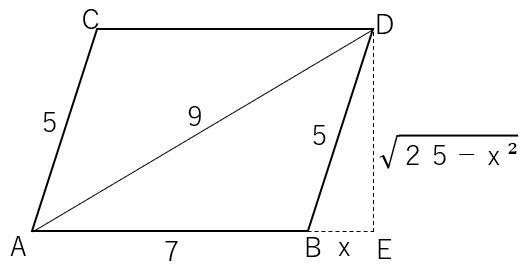 |  |
 |  | |
「平行四辺形 面積 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 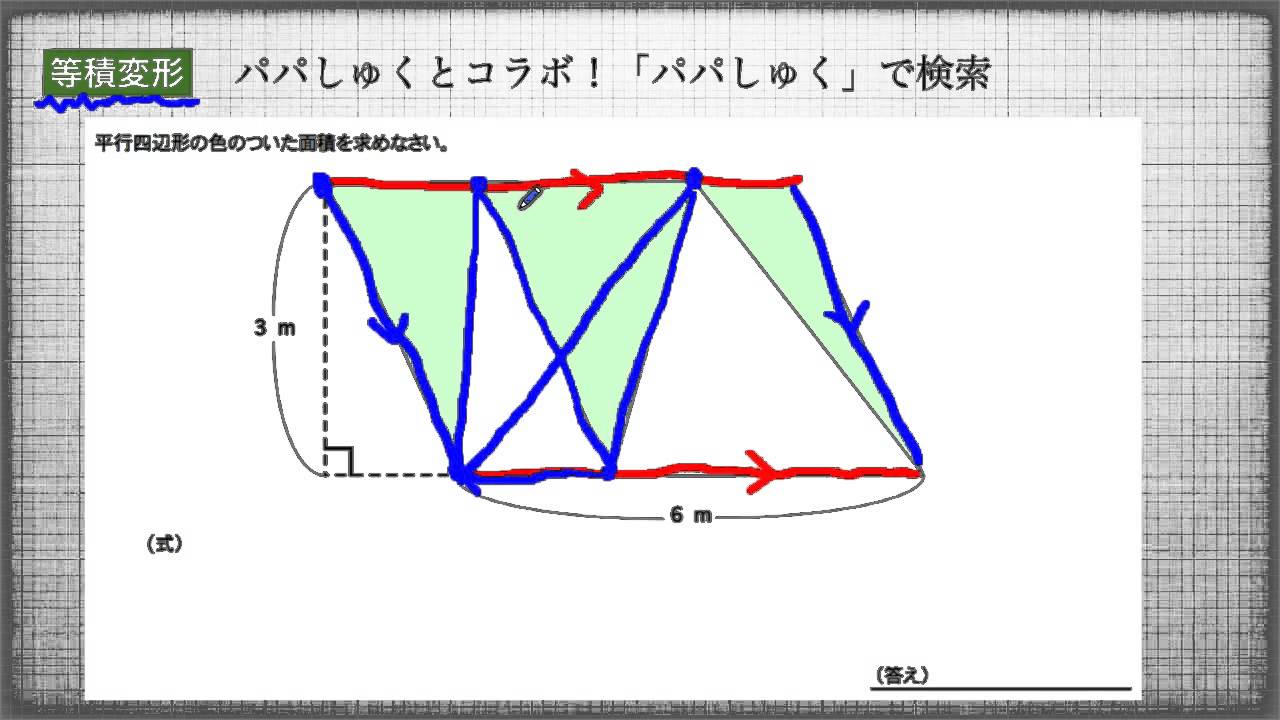 | 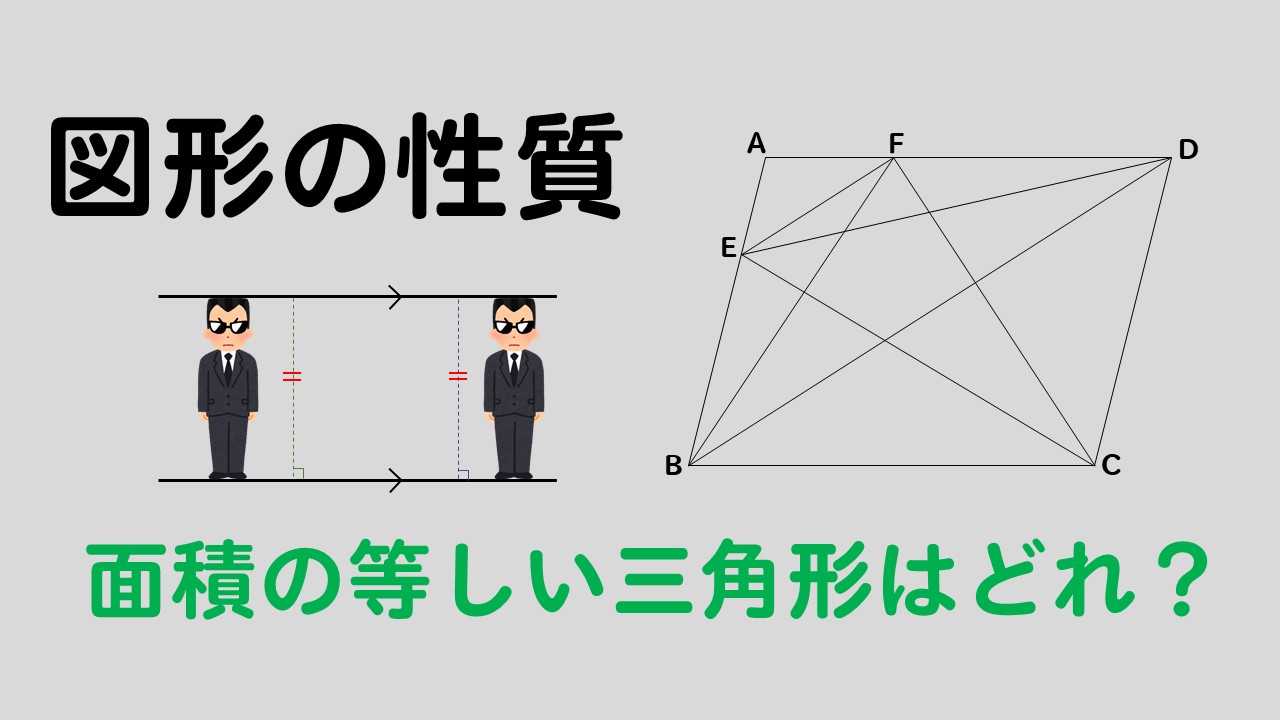 |
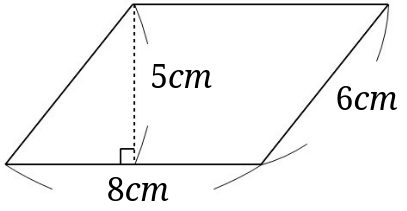 | 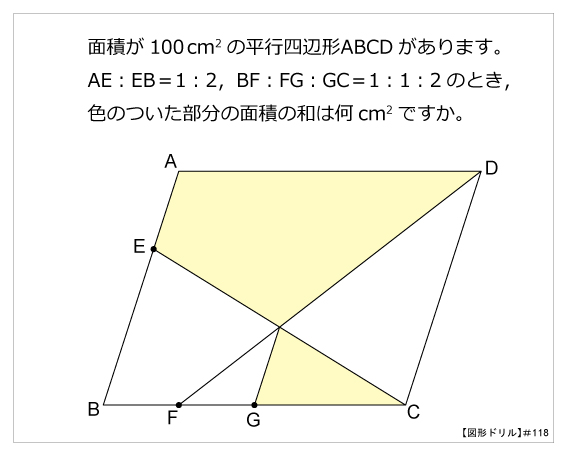 |  |
 |  | |
「平行四辺形 面積 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |
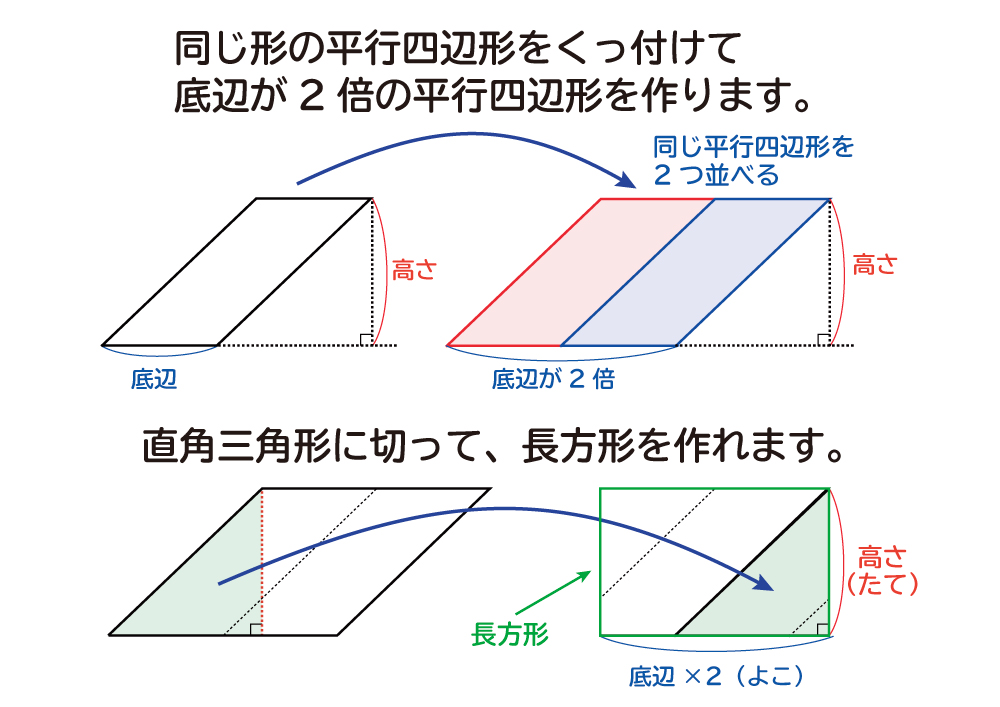
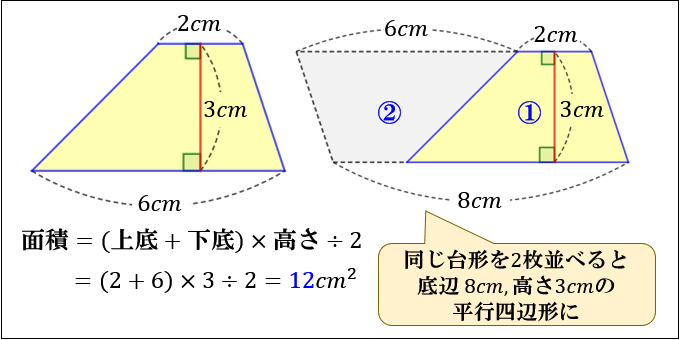
5年 平行四辺形の面積|算数イメージ動画集|大日本図書 平行四辺形の面積を求めるにはどうしたらいいでしょうか。 台形を2つ合わせて,あるいは三角形と台形を合わせて長方形にしてみると公式が使えます。 つまり,平行四辺形の面積は 底辺×高さ で 三角形、四角形の面積から、くふうして面積を求める問題です。 基本的な面積の求め方が分かっていれば解きやすい問題が多いので、よく出題されるパターンで練習して、確実に出来るようにしましょう。 よく出される問題 *色がついた部




